Project: Trees
In this project, we shall first do a relatively straightforward task in implementing a Binary Search Tree. Afterwards, we will be tackling a Chess related challenge.
Introduction
In our previous project, we were challenged with the implementation of a Linked List and Nodes; and we have learned just how instrumental Nodes are in creating a Linked List. Now we're back with our deadly Nodes knowledge and we're ready to take on Linked Lists much bigger cousins, the Tree. In this project, we shall first do a relatively straightforward task in implementing a Binary Search Tree.
Afterwards, we will be tackling a classic Chess related challenge, which could be treated like a tree, or like yet another data structure similar to trees.
Good luck, and be persistent. This will be a challenging exercise.
Project 1: Binary Search Trees
You have learned about binary search trees -- where you take a group of data items and turn them into a tree full of nodes where each left node is "lower" than each right node. The tree starts with the "root node" and any node with no children is called a "leaf node". You have also learned about tree traversal algorithms like breadth-first and depth-first.
Now, let's take a look at balanced binary search trees (BST). Read this article and watch this video to understand the basic algorithm used to build a balanced BST. Although these two resources do not use Ruby, you should understand it enough to develop your own pseudocode.
Assignment 1
You'll build a balanced BST in this assignment. Do not use duplicate values because they make it more complicated and result in trees that are much harder to balance. Therefore, be sure to always remove duplicate values or check for an existing value before inserting.
Build a
Nodeclass. It is should have attributes for the data it stores as well as its left and right children. As a bonus, try including theComparablemodule and make nodes compare using their data attribute.Build a
Treeclass which accepts an array when initialized. TheTreeclass should have arootattribute which uses the return value of#build_treewhich you'll write next.Write a
#build_treemethod which takes an array of data (e.g. [1, 7, 4, 23, 8, 9, 4, 3, 5, 7, 9, 67, 6345, 324]) and turns it into a balanced binary tree full ofNodeobjects appropriately placed (don't forget to sort and remove duplicates!). The#build_treemethod should return the level-1 root node.Write an
#insertand#deletemethod which accepts a value to insert/delete (you'll have to deal with several cases for delete such as when a node has children or not). If you need additional resources, check out these two articles on inserting and deleting, or this video with several visual examples.Write a
#findmethod which accepts a value and returns the node with the given value.Write a
#level_ordermethod that returns an array of values. This method should traverse the tree in breadth-first level order. This method can be implemented using either iteration or recursion (try implementing both!). Tip: You will want to use an array acting as a queue to keep track of all the child nodes that you have yet to traverse and to add new ones to the list (as you saw in the video).Write
#inorder,#preorder, and#postordermethods that returns an array of values. Each method should traverse the tree in their respective depth-first order.Write a
#heightmethod which accepts a node and returns its height. Height is defined as the number of edges in longest path from a given node to a leaf node.Write a
#depthmethod which accepts a node and returns the depth(number of levels) beneath the node.Write a
#balanced?method which checks if the tree is balanced. A balanced tree is one where the difference between heights of left subtree and right subtree of every node is not more than 1.Write a
#rebalancemethod which rebalances an unbalanced tree. Tip: You'll want to create a level-order array of the tree before passing the array back into the#build_treemethod.Write a simple driver script that does the following:
Create a binary search tree from an array of random numbers (
Array.new(15) { rand(1..100) })Confirm that the tree is balanced by calling
#balanced?Print out all elements in level, pre, post, and in order
try to unbalance the tree by adding several numbers > 100
Confirm that the tree is unbalanced by calling
#balanced?Balance the tree by calling
#rebalanceConfirm that the tree is balanced by calling
#balanced?Print out all elements in level, pre, post, and in order
Tip: If you would like to visualize your binary search tree, here is a #pretty_print method:
Project 2: Knight's Travails
Now you're a pro with DFS and BFS. Let's try using our search algorithms on a real problem.
For this project, you'll need to use a data structure that's similar (but not identical) to a binary tree. For a summary of a few different examples, reference this article.
A knight in chess can move to any square on the standard 8x8 chess board from any other square on the board, given enough turns (don't believe it? See this animation). Its basic move is two steps forward and one step to the side. It can face any direction.
All the possible places you can end up after one move look like this:
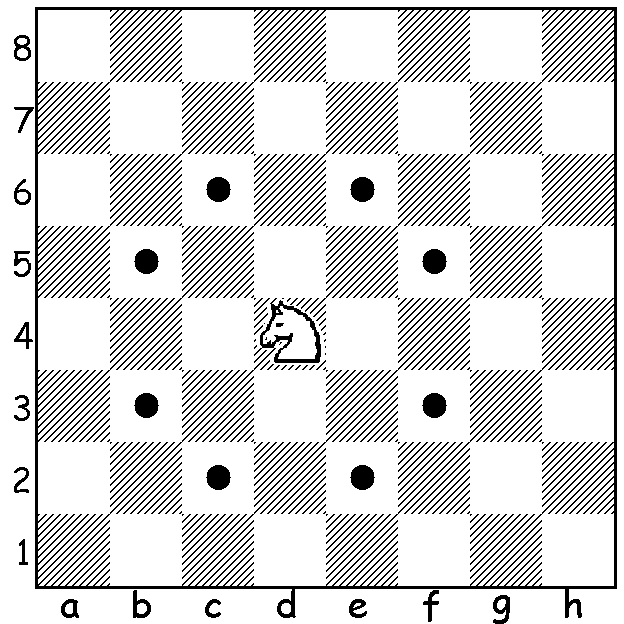
Assignment 2
Your task is to build a function knight_moves that shows the simplest possible way to get from one square to another by outputting all squares the knight will stop on along the way.
You can think of the board as having 2-dimensional coordinates. Your function would therefore look like:
knight_moves([0,0],[1,2]) == [[0,0],[1,2]]knight_moves([0,0],[3,3]) == [[0,0],[1,2],[3,3]]knight_moves([3,3],[0,0]) == [[3,3],[1,2],[0,0]]Put together a script that creates a game board and a knight.
Treat all possible moves the knight could make as children in a tree. Don't allow any moves to go off the board.
Decide which search algorithm is best to use for this case. Hint: one of them could be a potentially infinite series.
Use the chosen search algorithm to find the shortest path between the starting square (or node) and the ending square. Output what that full path looks like -- here's an example:
Last updated